種の多様性は、群集の中の種の数(richness)と種間の均等性(evenness)の 2 つの要素が関与している。例えば、地域 A と地域 B の 10m2 区画中の昆虫を調査した結果、次のようなデータが得られたとする。このデータから、地域 A と地域 B の昆虫の種の多様性は、richness は同じだが、evenness が異なることが示唆される。種の多様性を測る指標として、様々な指標が提案されているが、データの evenness によって間違った推測をしてしまう場合がある。
| 昆虫 a | 昆虫 b | 昆虫 c | 昆虫 d | 昆虫 e | |
| 地域 A | 10 | 10 | 10 | 10 | 10 |
| 地域 B | 25 | 21 | 1 | 1 | 1 |
種数面積曲線 species-area curve
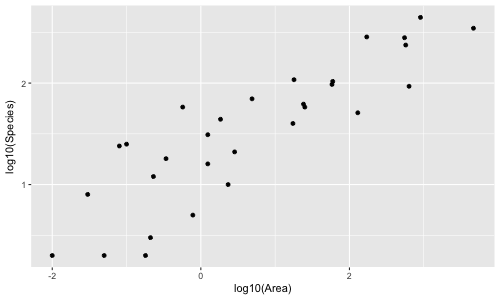
調査対象領域の面積が大きくなると、その領域で生息する生物の種数も多くなる。横軸を調査対象領域の面積として、縦軸を生物種の数としてプロットしたグラフを種数面積曲線という。横軸と縦軸を対数スケールにすると、ほぼ直線になる。種数面積曲線は次のように数式で表せる。
\[ S=cA^{z} \]S は生物種の数で、A は調査対象領域の面積を表す。c および z は定数で、それらの値は生物種や調査地域によって異なる。
相対優占度曲線 relative abundance curve
相対優占度曲線は、相対的な種の多様性を表すグラフである。縦軸に全個体数に対するある種の個体数の割合を、横軸に種の個体数の多さでランクづけられた順位をプロットする。
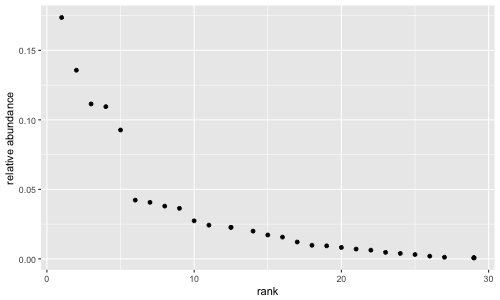
相対優占度曲線は、複数の地域の種の多様性を比較したいときに利用する。1 つの地域につき 1 つの相対優占度曲線を描き、複数の相対優占度曲線の形で、各地域の種の多様性を比較する。種の多様性が大きければ、右に伸びるような形をとる。逆に、種の多様性が小さければ、下に急に下がるような形をとる。
シャノン=ウィーバーの多様度指数 Shannnon-Wiener index
シャノン=ウィーバーの多様度指数は、種の多様性を測る指標として利用されている。種の数を S、種 i の相対的占優度を pi とすると、シャノン=ウィーバーの多様度指数は次のように計算される。
\[ H = -\sum_{j=1}^{S}p_{i}\log_{10} p_{i} \]データに稀な種を多く含まれるとき(数個体しかない種が大量に存在するとき)、シャノン=ウィーバーの多様度指数は過大評価してしまう可能性がある。
シンプソンの多様度指数 Shannnon-Wiener index
シンプソンの多様度指数は、種の多様性を測る指標として利用されている。種の数を S、種 i の相対的占優度を pi とすると、シンプソンの多様度指数は次のように計算される。
\[ D=1-\sum_{j=1}^{S}p_{i}^{2} \]