近交係数 (inbreeding coefficient) は、ある個体が持つ 2 つのアレル(相同遺伝子)が、共通の祖先の同一遺伝子に由来する確率である。同祖遺伝子 (identical by descent; IBD) あるいはオート接合 (autozygous) などの用語を用いば、近交係数は、ある個体が持つ 2 つのアレルが同祖遺伝子である確率、あるいはある個体が持つ 2 つのアレルがオート接合である確率と言い換えることができる。ここでいう同祖遺伝子とは、同一祖先に由来する遺伝子のことである。また、同祖遺伝子のホモ接合をオート接合といい、そうでない遺伝子のホモ接合をアロ接合 (allozygote) という。
近交係数の計算例
ここで近交係数を計算する例をみていく。まず、次図に示すような、個体 A が持つ 2 つのアレルが祖先の個体 R の同一アレルに由来する確率、すなわち個体 A の近交係数を考える。
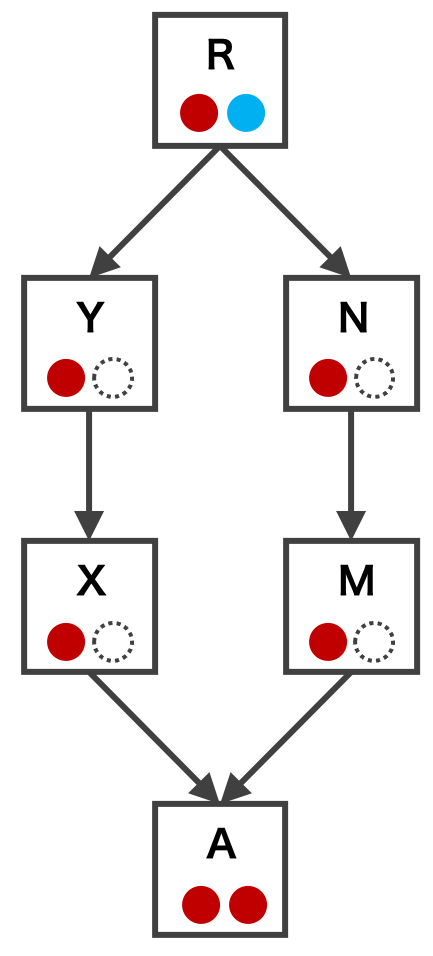
例えば個体 A が持つ 2 つのアレルが R の赤色アレルに由来するのであれば、R の赤色アレルが R → Y → X → A かつ R → N → M → A の 2 つのルートを介して同時に伝わってくる必要がある。水色についても同様に考えることができる。ここで、まず、R から Y および N にアレルが伝わる確率を考えてみる。R から Y に赤色アレルかつ R から N にも赤色アレルが伝わる確率は (1/2)(1/2)=1/4 である。同様に、R から Y に水色アレルかつ R から N にも水色アレルが伝わる確率も 1/4 である。次に、少し複雑な、「R から Y に赤色アレルかつ R から N に水色アレルが伝わり」かつ「赤色アレルと水色アレルが共通祖先の同一アレルに由来する」確率を考える。前者の「R から Y に赤色アレルかつ R から N に水色アレルが伝わる」確率は (1/2)(1/2)=1/4 でと計算できる。後者の「赤色アレルと水色アレルが共通祖先の同一アレルに由来する」確率は計算できないが、これは個体 R の近交係数そのものである。ここで、個体 R の近交係数を FR とくと、「R から Y に赤色アレルかつ R から N に水色アレルが伝わり」かつ「赤色アレルと水色アレルが共通祖先の同一アレルに由来する」確率は (1/4)FR と書ける。同様にして、「R から Y に水色アレルかつ R から N に赤色アレルが伝わり」かつ「赤色アレルと水色アレルが共通祖先の同一アレルに由来する」確率も (1/4)FR である。
次に、仮に、個体 R の赤色アレルが個体 Y および個体 N に伝わった時、その赤色アレルが Y → X、X → A、N → M、M → A へと伝わる確率はすべて 1/2 である。以上により、個体 A の近交係数は次のように求めることができる。
\[ \begin{eqnarray} F_{A} &=& Pr(R \to Y, R \to N) Pr(Y\to X) Pr(X\to A) Pr(N\to M) Pr(M \to A) \\ &=& \left(\frac{1}{4} + \frac{1}{4} + \frac{1}{4}F_{R} + \frac{1}{4}F_{R} \right) \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \\ &=& \left( \frac{1}{2} \right)^{5}\left(1 + F_{R}\right) \end{eqnarray} \]次にもう少し複雑な例を見ていく。下図のような、祖先 R および祖先 S が存在したときに、個体 A の近交係数を求めてみる。
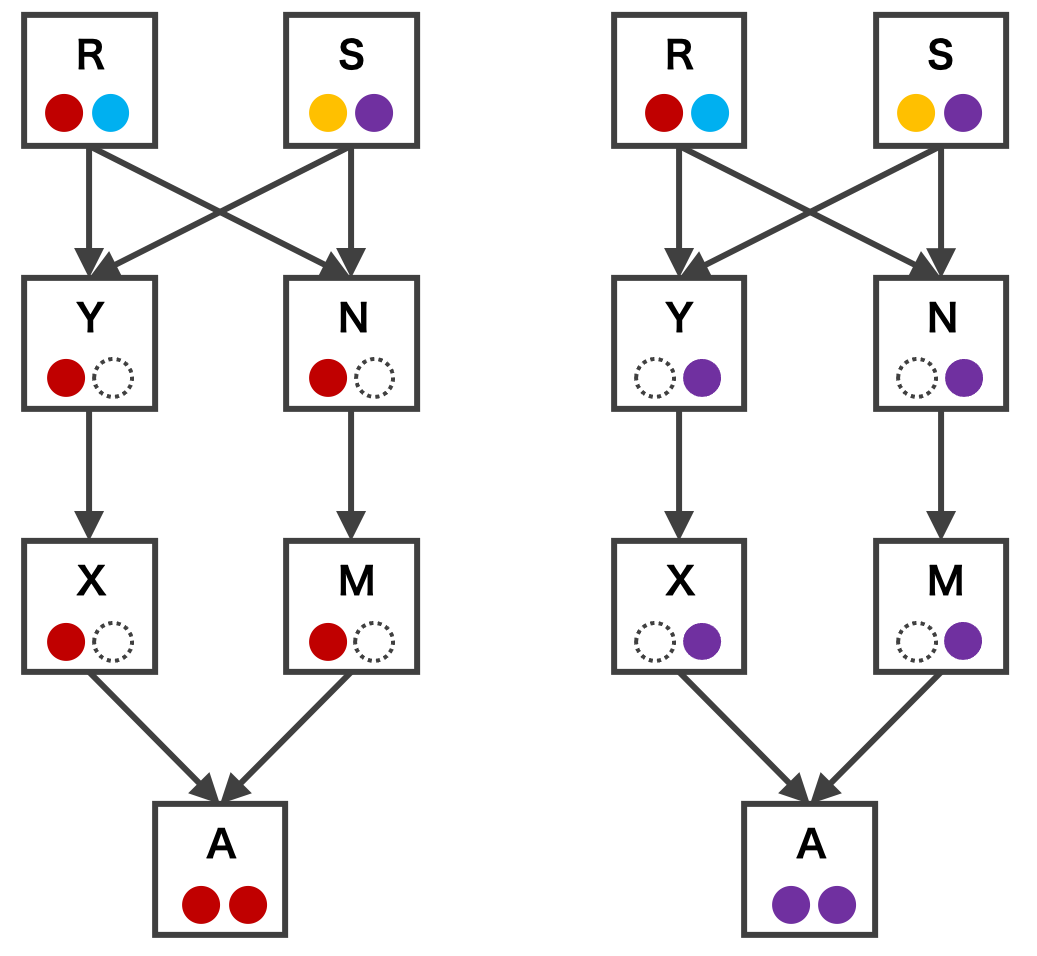
まず、祖先 S を無視して、祖先 R だけを考える。これは上で見た例と同じように近交係数を計算できる。次に、祖先 R を無視して、祖先 S だけを考える。これも上で見た例と同じように近交係数を計算できる。両者は互いに排反であるので、個体 A の近交係数は次のように計算できる。 \[ \begin{eqnarray} F_{A} &=& Pr(R \to Y, R \to N) Pr(Y\to X) Pr(X\to A) Pr(N\to M) Pr(M \to A) \\ && + Pr(S \to Y, S \to N) Pr(Y\to X) Pr(X\to A) Pr(N\to M) Pr(M \to A) \\ &=& \left( \frac{1}{2} \right)^{5}\left( \left(1 + F_{R}\right) + \left(1 + F_{S}\right) \right) \end{eqnarray} \]
ライト・フィッシャー集団における近交係数
ライト・フィッシャー集団は理想的に進化する集団である。この集団において、ある世代 t から次の世代 t + 1 を作り出すには、まず t 世代において N 個体の二倍体からランダムに 2 個体を選ぶ。次に、それぞれの個体からアレル 1 つずつ取り出して、これを t + 1 世代の 1 個体のアレルとする。このような操作を N 回繰り返していき、t + 1 世代の N 個体を得る。
このような集団におて、t 世代の任意の個体の近交係数 Ft を考える。t 世代の個体数が N 個体であり、親世代(t-1 世代)の個体数も N 個体である。この集団は二倍体なので、アレルは 2N 個ある。① t 世代にある任意の 2 つのアレルが、親世代(t - 1 世代)の同一アレルに由来する確率は、1 · (1/2N) である。また、② t 世代にある任意の 2 つの配偶子が親世代の異なるアレルに由来する確率は 1 - 1 · (1/2N) である。この「親世代の異なるアレル」が同じ祖先に由来する確率は Ft-1 である。よって、「t 世代にある任意の 2 つのアレルが親世代の異なるアレルに由来し」かつ「両者が共通祖先の同一アレルに由来する」確率は (1 - 1 · (1/2N))Ft-1 である。①および②が互いに排反であるので、以上により、t 世代の任意の個体の近交係数 Ft は次のように計算できる。
\[ F_{t} = \frac{1}{2N} + \left(1 - \frac{1}{2N}\right) F_{t-1} \]この漸化式は、初項が 1 で、比が 1 - (1/2N) の等比数列であることに着目し、漸化式をとくと、
\[ \begin{eqnarray} F_{t} &=& \frac{1}{2N} + \left(1 - \frac{1}{2N}\right) F_{t-1} \\ &=& \frac{1}{2N} + \left(1 - \frac{1}{2N}\right) \left( \frac{1}{2N} + \left(1 - \frac{1}{2N}\right) F_{t-2} \right) \\ &=& \frac{1}{2N} + \frac{1}{2N}\left(1 - \frac{1}{2N}\right) + \left(1 - \frac{1}{2N}\right)^{2} F_{t-2} \\ &=& \frac{1}{2N} + \frac{1}{2N}\left(1 - \frac{1}{2N}\right) + \frac{1}{2N}\left(1 - \frac{1}{2N}\right)^{2} + \cdots \\ &=& \frac{1}{2N}\sum^{t-1}_{j=0}\left(1-\frac{1}{2N}\right)^{j} \\ &=& 1 - \left(1 - \frac{1}{2N}\right)^{t} \end{eqnarray} \]ここで定数 1 を移行して式を整理すると
\[ 1 - F_{T} = \left(1 - \frac{1}{2N}\right) \left( 1 - F_{t-1}\right) \]よって、
\[ 1 - F_{T} = \left( 1 - \frac{1}{2N} \right)^{t} \left(1 - F_{0}\right) \]F0 = 0 により、FT は次のように求めることができる。
\[ F_{t} = 1-\left(1 - \frac{1}{2N}\right)^{t} \] この式は、次のように近似できる。このことから、世代交代が繰り返されると、近交係数が 1 に収束することがわかる。 \[ F_{t} = 1 - \left(1 - \frac{1}{2N}\right)^{t} \sim 1 - \exp\left(-\frac{t}{2N}\right) \]無限サイトモデル
次に無限サイトモデル (infinite site model) における近交係数を求める。無限サイトモデルとは、世代ごとに塩基配列に突然変異が確率 u で起こり、かつこの確率 u は非常に小さいために、突然変異が 2 回起きて元の塩基配列にもどることができないと仮定したモデルである。このモデルにおいて、両親から受け取ったアレルの両方に突然変異が起こらない確率が (1-u)2 であることから、t 世代における近交係数は次のように計算できる。
\[ F_{t} = \left[ \frac{1}{2N} + \left( 1 - \frac{1}{2N}\right)F_{t-1} \right] (1-u)^2 \]このモデルにおいて平衡状態に達したとき、Ft = Ft-1 となる。さらに u が無視できるほど十分に小さいとき、上の式をとくと、平衡状態における近交係数の推定値は次のように計算できる。
\[ \begin{eqnarray} \hat{F} &=& \frac{(1-u)^{2}}{2N - (2N-1)(1-u)^2} \\ &=& \frac{1 - 2u + u^{2}}{2N - (2N-1) + 2(2N-1)u - (2N-1)u^2} \\ & \approx & \frac{1}{4Nu+1} \end{eqnarray} \]\(\hat{F}\) は集団の中からランダムに選んだ 2 つのアレルが同じである割合の推定値である。これに対して、ランダムに選んだ 2 つのアレルが異なっている確率 \(\hat{H}\) は次のように計算でき、これをヘテロ接合度 (heterozygosity) とよぶ。
\[ \hat{H} = 1-\hat{F} =\frac{4Nu}{4Nu+1} \]なお、4Nu は集団内の遺伝的多様性を表す変数であり、集団変異率とよばれたりする。また、この変数は遺伝学において非常に重要であるため、θ で書き表されることが多い。
\[ \theta = 4Nu \]