自然選択 (natural selection) は、生物が生息環境に適応するに至った過程を説明する理論の一つである。具体的に、生存に有利な遺伝子型が集団内で保存され、有害な遺伝子型が除去される、を説明する理論である。1850 年代にダーウィンとウォーレスによって初めて提唱された。自然選択の事例として、次のようなものが有名である。
- 高いところの葉を食べるのに有利な、長い首を持つキリンが生き残った。
- ダーウィンフィンチが乾季に木の実を食べるのに適した大きな嘴を持った個体が生き残り、雨季に大きな嘴を持った個体が減る。
- 農薬などの散布で、その農薬に対する薬剤抵抗性を持った個体の子孫が生き残って繁栄する。
自然選択の種類
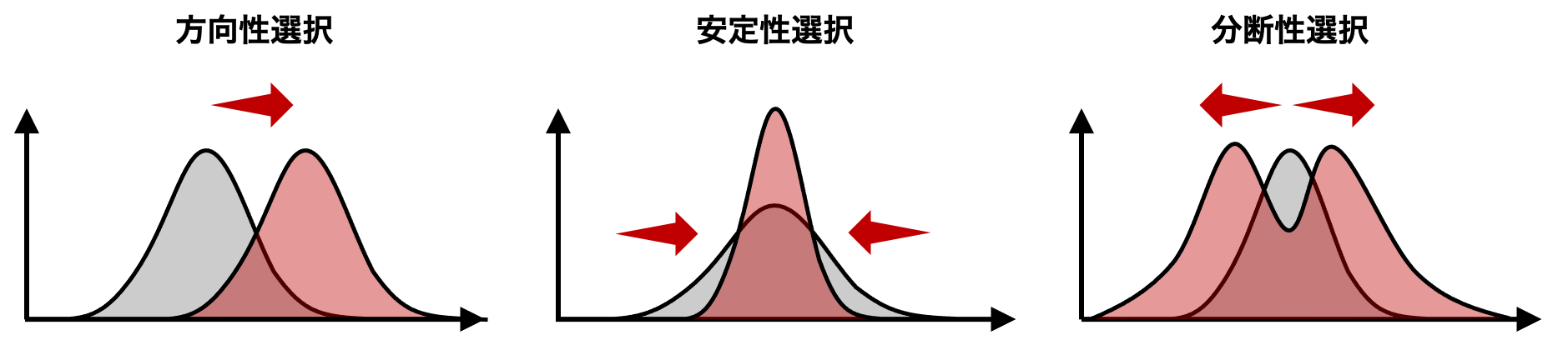
自然選択は選択の働く方向によって方向性選択、安定化選択(平衡選択)、分断選択(多様化選択)に分けることができる。 方向性選択 (directinal selection) は、最適な形質が集団の外にあり、集団の形質がそこに向かうように働く。キリンの首の長さの進化や工業暗化による蛾の色の変化などが方向性選択の一例と言える。安定性選択 (stabilizing selection) は、形質の分布の両端から個体を取り除き、世代が変わっても同じ平均を保つように働く。キリンの首の長さは、今では安定性選択により、長くも短くもならないといえる。あるいは、鎌状赤血球症に関わるアレルが貧血症にかかるコストとマラリアにかかるコストの両方(両端)から遠ざかるように中央に落ち着く。分断選択 (disruptive selection) は、一つの集団の形質の最適値が複数あり、形質の分布がそれぞれの最適値に分離していくように働く。
適応
自然選択により生き残った生物が、その環境に適した生態や形態を持つようになることを適応といい、その度合いを適応度 (fitness) という。具体的に、個体が子供をどれだけ残せるのかを示す量となっている。集団の中に、多型なアレルが存在し、それらのアレルの適応度に差があるとき(すなわち生存や繁殖に有利・不利があるとき)に、自然選択が働いていると言える。
自然選択には正の選択 (positive selection) と負の選択 (negative selection) がある。あるアレルが他のアレルに比べ適応度が高く、集団全体に広がっていく場合の自然選択を正の選択という。逆に、あるアレルが生存にとって不利であるとき、そのアレルが集団から徐々に除去される。このような自然選択を負の選択という。正の選択と負の選択は相対的なものであり、例えば、突然変異によって生じた少数のアレルが正の選択となった場合、既存の野生型のアレルが負の選択となる。
あるアレルに対して正の選択が働いた場合、生存に有利なアレルが集団に急速に固定される。すると、そのアレルの近傍領域にある塩基も一緒に集団中に広がる。そのため、そのアレルの周りの領域において、遺伝的多様性が減ることが考えられる。この効果をセレクティブスウィープ (selective sweep) という。逆に、あるアレルに対して負の選択が働いした場合、そのアレルは集団から取り除かれる。その過程で、アレルの周りの領域の多様性が減ってくる。この効果をバックグラウンドセレクション (background selection) という。ただ、実際問題としてセレクティブスウィープとバックグラウンドセレクションが似ているので、両者を区別するのが難しい。
適応度とアレル頻度の変化
集団内において、適応度の高いアレルを持つ個体は生存および繁殖確率が相対的に高く、そのアレルが集団に固定されやすい。実際に、世代間での適応度の変化が、適応度にどのように影響されるのかを計算してみる。
あるアレル A および a を考える。A および a のアレル頻度をそれぞれ p および q (= 1 - p) とする。このとき、ハーディ・ワインベルグ平衡において、次世代のハプロタイプの AA、Aa、および aa の頻度はそれぞれ
\[ Pr(AA) = Pr(A)^{2} = p^{2} \] \[ Pr(Aa) = 2Pr(A)Pr(a) = 2pq \] \[ Pr(aa) = Pr(a)^{2} = q^{2} \]アレル A およびアレル a の適応度が同じであれば、各ハプロタイプの頻度は上式のように成り立つ。しかし、例えば一方の A が他方の a に比べ適応度が高かったりする場合は、A を持つ個体が多くの子孫を残すことができ、次の世代においてアレル A を持つ個体が多くなると考えられる。そこで、ハプロタイプ AA、Aa、aa の適応度をそれぞれ wAA、 wAa、 waa としたとき、自然選択が働いているときに、次世代のハプロタイプ AA、Aa、aa の頻度は次のようになると考えられる。
\[ Pr(AA) = p^{2}w_{AA} \] \[ Pr(Aa) = 2pq w_{Aa} \] \[ Pr(aa) = q^{2}w_{aa} \]このとき、t 世代および t + 1 世代におけるアレル A の頻度を Prt(A) と Prt+1(A) としたとき、両者をあらためてアレル頻度 p および q で表すと次のようになる。
\[ Pr_{t}(A) = Pr_{t}(AA) + \frac{1}{2}Pr_{t}(Aa) = p^{2} + pq \] \[ Pr_{t+1}(A) = Pr_{t+1}(AA) + \frac{1}{2}Pr_{t+1}(Aa) = \frac{p^{2}w_{AA} + pqw_{Aa}}{\bar{w}} \]なお、\(\bar{w}\) は平均適応度と呼ばれ、次のように表される。
\[ \bar{w} = p^{2}w_{AA} + 2pqw_{Aa} + q^{2}w_{aa} \]このとき、世代 t から世代 t + 1 に変化していったとき、アレル A の頻度の変化は次のように求めることができる。
\[ \Delta Pr(A) = Pr_{t+1}(A) - Pr_{t}(A) = \frac{pq\left( p(w_{AA}-w_{Aa}) + q(w_{Aa} - w_{aa}) \right)}{\bar{w}} \]方向性選択
方向性選択において、世代間でアレル頻度がどのように変化していくのかを見ていく。ハプロタイプの AA、Aa、aa の頻度をそれぞれ 1、1 - hs、1 - s とおく。s は淘汰係数 (selection coefficient) とよばれ、h は優性度 (degree of dominance) とよばれる。このとき、wAA = 1、wAa = 1 - hs、waa = 1 - s を ΔPr(A) に代入すると、
\[ \begin{eqnarray} \Delta Pr(A) &=& \frac{pq\left( p(w_{AA}-w_{Aa}) + q(w_{Aa} - w_{aa}) \right)}{\bar{w}} \\ &=& \frac{spq\left(hp + (1-h)q\right)}{\bar{w}} \end{eqnarray} \]h = 0 のとき A が完全優性であり、h = 1 のとき A が完全劣性である。
安定性選択(平衡選択)
安定性選択において、アレルの頻度がどのように変化していくのかをみていく。
超優性
ハプロタイプの AA、Aa、aa の頻度をそれぞれ 1 - t、1、1 - s とおく。s および t は淘汰係数である。このとき、ΔPr(A) は次のように計算される。
\[ \begin{eqnarray} \Delta Pr(A) &=& \frac{pq\left( p(w_{AA}-w_{Aa}) + q(w_{Aa} - w_{aa}) \right)}{\bar{w}} \\ &=& \frac{pq\left(t (s+t)p\right)}{\bar{w}} \end{eqnarray} \]半優性
ハプロタイプの AA、Aa、aa の頻度をそれぞれ 1、1 + s、1 + 2s とおく。s は淘汰係数である。このとき、ΔPr(A) は次のように計算される。
\[ \begin{eqnarray} \Delta Pr(A) &=& \frac{pq\left( p(w_{AA}-w_{Aa}) + q(w_{Aa} - w_{aa}) \right)}{\bar{w}} \\ &=& \frac{q\left(q(1+2s) + p(1+s) \right)}{\bar{w}}-q \end{eqnarray} \]