biology

遺伝的浮動

遺伝的浮動 (random genetic drift) は、生物集団（個体群）にみられる現象で、世代を重ねている間に、遺伝子頻度が変動する説明する概念である。有限な集団において、次世代に伝えるアレルをランダムに抽出する過程で、比較的に少数のアレルだけが抽出されることがある。このような効果が累積していったときに、この集団の遺伝子頻度が特定のアレルに偏るようになり、場合によって他方のアレルが消失したりする。このことをモデル化したものがライト・フィッシャーモデル (Wright-Fisher model) である。

ライト・フィッシャーモデル

ライト・フィッシャーモデル (Wright-Fisher model) あるいはライト・フィッシャー集団 (Wright-Fisher population) では、任意交配を行う有限集団であり、次世代の遺伝子がこの集団からランダムに抽出される。N 個体からなるライト・フィッシャー集団から次世代の N 個体を作り出すには、例えば、次のような手順に従って行うことができる。

  1. 集団の中からランダムに 2 個体を抽出する。
  2. 抽出した 2 個体それぞれからランダムにアレルを 1 つ抽出し、両者を合わせて次世代の個体の持つアレルとする。
  3. 手順 1-2 を N 回繰り返す。

N 個体の二倍体からなる集団を考える。このとき、あるアレルについて考える。このアレルは m 種類存在し、それらを A1、A2、…、Am とする。それぞれのアレルの頻度を p1、p2、…、pm とする。ここで t 世代におけるアレル頻度が与えられたとき、t + 1 世代の集団にアレル Ai が k 個含まれる確率は、次のように計算される。

\[ P_{A_{i}}(k) = \begin{pmatrix} 2N \\ k \end{pmatrix} p_{i}^{k}(1- p_{i})^{2N-k} \]

この分布が二項分布であり、その平均は 2Npi であり、分散は 2Npi(1 - pi) である。つまり、t + 1 世代においてアレル Ai の個数（の期待値）が 2Npi となる。また、N が十分に大きく、pi が十分に小さければ、上式はポアソン分布に近似できるため、

\[ P_{A_{i}}(k) = \frac{(2Np_{i})^{k!}}{i}e^{-2Np_{i}} \]

アレル頻度が 0 または 1 に収束する（変異が集団から消えるまたは固定される）ことを、Python でシミュレーションを行ってみる。まず、集団サイズが 1000 の二倍体を想定し、AA の遺伝子型を持つ個体数を 50%、Aa の遺伝子型を持つ個体数を 40%、そして aa の遺伝子型を持つ個体数を 10% とする。1000 世代の世代交代を繰り返したときに各世代におけるアレル a の頻度を計算して可視化する。そして、このシミュレーションを独立に 10 回行う。シミュレーションの結果は次のようになる。

import copy
import matplotlib.pyplot as plt
import random
random.seed(1234)

N = 1000
t0 = []
t0.extend([[0, 0] for i in range(int(N * 0.50))])
t0.extend([[0, 1] for i in range(int(N * 0.30))])
t0.extend([[1, 1] for i in range(int(N * 0.20))])
random.shuffle(t0)

def generate_next(population):
  f1_population = []
  for i in range(len(population)):
    xx, xy = random.sample(population, 2)
    x = random.sample(xx, 1)[0]
    y = random.sample(xy, 1)[0]
    f1 = [x, y]
    f1_population.append(f1)
  return f1_population


def calc_freq(population):
  n = 0
  n0 = 0
  for xx in population:
    n += 2
    for x in xx:
      if x == 0:
        n0 += 1
  return n0 / n


simulate_freq = []
for n in range(10):
  population = copy.deepcopy(t0)
  _sim_freq = [calc_freq(population)]
  for i in range(1000):
    population = generate_next(population)
    _sim_freq.append(calc_freq(population))
  simulate_freq.append(_sim_freq)


fig = plt.figure(figsize=(10, 4), dpi=200)
ax = fig.add_subplot()
for sim_i in simulate_freq:
  ax.plot([i for i in range(len(sim_i))], sim_i)


plt.show()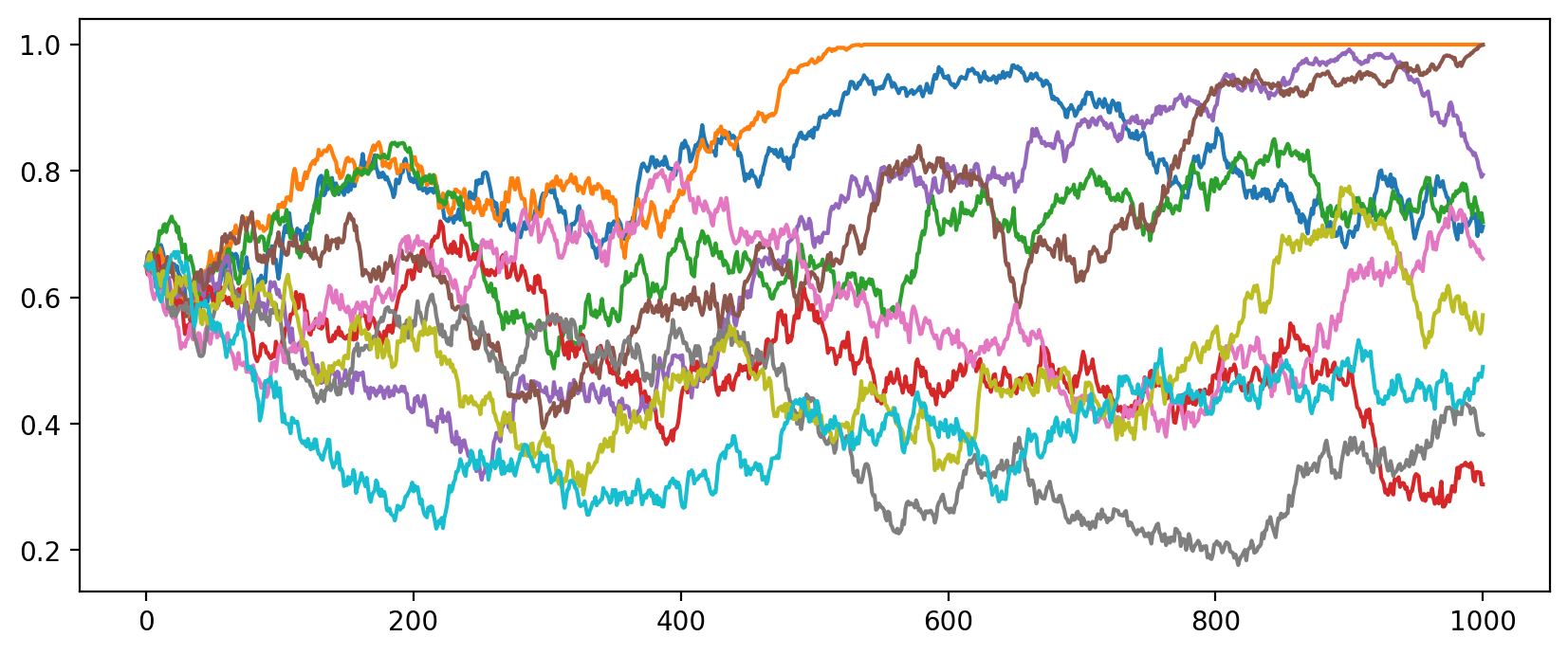
集団サイズが大きい時のライト・フィッシャー集団のシミュレーション

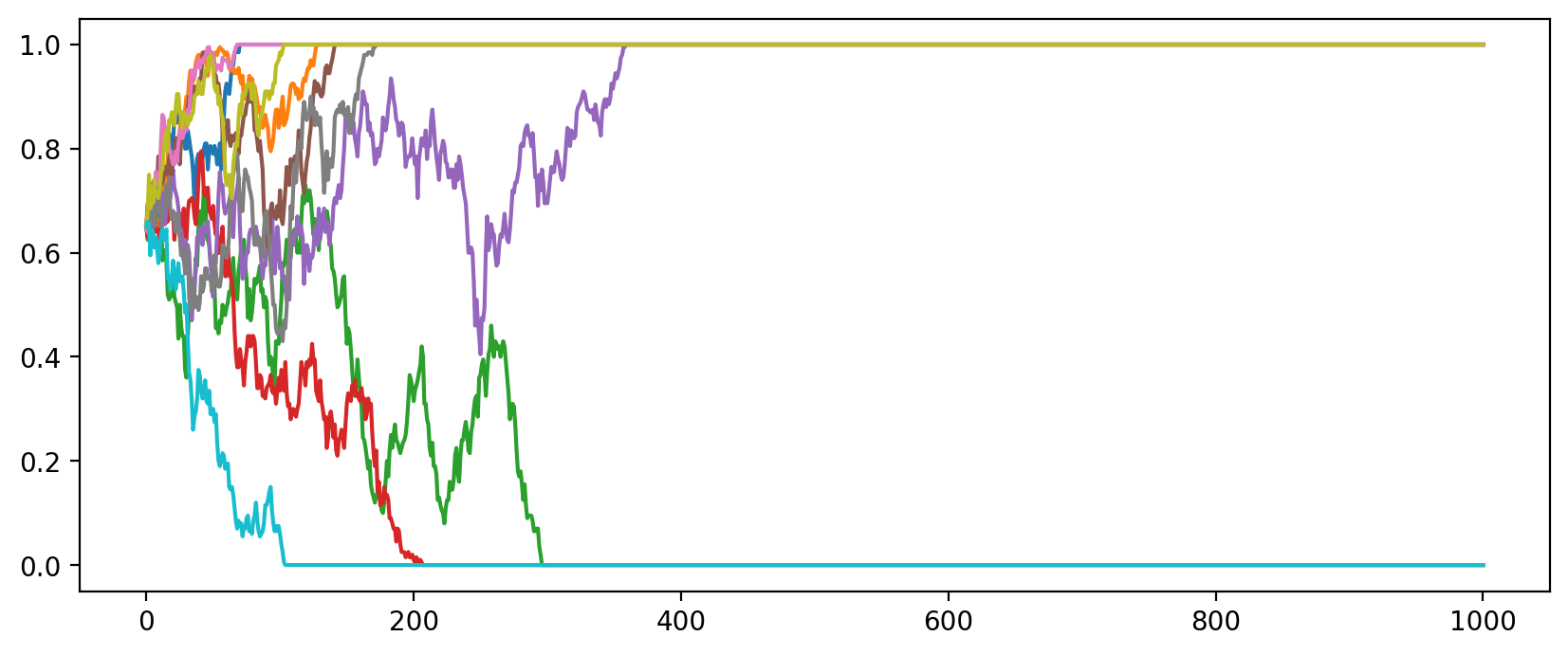
集団サイズを 100 に設定して、他の条件を変化させないときは、このような結果となる。集団サイズが小さいとき、変異がより早く集団から消えるか、固定されることになる。

集団サイズが小さい時のライト・フィッシャー集団のシミュレーション